utilities¶

Returns a synchronized shared array

Return evenly spaced values within a given interval.

Values are generated within the half-open interval [start, stop) (in other words, the interval including start but excluding stop). For integer arguments the function is equivalent to the Python built-in range function, but returns an ndarray rather than a list.

When using a non-integer step, such as 0.1, the results will often not be consistent. It is better to use linspace for these cases.

start : number, optional

Start of interval. The interval includes this value. The default start value is 0.

stop : number

End of interval. The interval does not include this value, except in some cases where step is not an integer and floating point round-off affects the length of out.

step : number, optional

Spacing between values. For any output out, this is the distance between two adjacent values, out[i+1] - out[i]. The default step size is 1. If step is specified, start must also be given.

dtype : dtype

The type of the output array. If dtype is not given, infer the data type from the other input arguments.

arange : ndarray

Array of evenly spaced values.

For floating point arguments, the length of the result is ceil((stop - start)/step). Because of floating point overflow, this rule may result in the last element of out being greater than stop.

linspace : Evenly spaced numbers with careful handling of endpoints. ogrid: Arrays of evenly spaced numbers in N-dimensions. mgrid: Grid-shaped arrays of evenly spaced numbers in N-dimensions.

>>> np.arange(3)
array([0, 1, 2])
>>> np.arange(3.0)
array([ 0.,  1.,  2.])
>>> np.arange(3,7)
array([3, 4, 5, 6])
>>> np.arange(3,7,2)
array([3, 5])

Create an array.

object : array_like

An array, any object exposing the array interface, an object whose __array__ method returns an array, or any (nested) sequence.

dtype : data-type, optional

The desired data-type for the array. If not given, then the type will be determined as the minimum type required to hold the objects in the sequence. This argument can only be used to ‘upcast’ the array. For downcasting, use the .astype(t) method.

copy : bool, optional

If true (default), then the object is copied. Otherwise, a copy will only be made if __array__ returns a copy, if obj is a nested sequence, or if a copy is needed to satisfy any of the other requirements (dtype, order, etc.).

order : {‘C’, ‘F’, ‘A’}, optional

Specify the order of the array. If order is ‘C’, then the array will be in C-contiguous order (last-index varies the fastest). If order is ‘F’, then the returned array will be in Fortran-contiguous order (first-index varies the fastest). If order is ‘A’ (default), then the returned array may be in any order (either C-, Fortran-contiguous, or even discontiguous), unless a copy is required, in which case it will be C-contiguous.

subok : bool, optional

If True, then sub-classes will be passed-through, otherwise the returned array will be forced to be a base-class array (default).

ndmin : int, optional

Specifies the minimum number of dimensions that the resulting array should have. Ones will be pre-pended to the shape as needed to meet this requirement.

out : ndarray

An array object satisfying the specified requirements.

empty, empty_like, zeros, zeros_like, ones, ones_like, fill

>>> np.array([1, 2, 3])
array([1, 2, 3])

Upcasting:

>>> np.array([1, 2, 3.0])
array([ 1.,  2.,  3.])

More than one dimension:

>>> np.array([[1, 2], [3, 4]])
array([[1, 2],
       [3, 4]])

Minimum dimensions 2:

>>> np.array([1, 2, 3], ndmin=2)
array([[1, 2, 3]])

Type provided:

>>> np.array([1, 2, 3], dtype=complex)
array([ 1.+0.j,  2.+0.j,  3.+0.j])

Data-type consisting of more than one element:

>>> x = np.array([(1,2),(3,4)],dtype=[('a','<i4'),('b','<i4')])
>>> x['a']
array([1, 3])

Creating an array from sub-classes:

>>> np.array(np.mat('1 2; 3 4'))
array([[1, 2],
       [3, 4]])

>>> np.array(np.mat('1 2; 3 4'), subok=True)
matrix([[1, 2],
        [3, 4]])

Convert the input to an array.

a : array_like

Input data, in any form that can be converted to an array. This includes lists, lists of tuples, tuples, tuples of tuples, tuples of lists and ndarrays.

dtype : data-type, optional

By default, the data-type is inferred from the input data.

order : {‘C’, ‘F’}, optional

Whether to use row-major (C-style) or column-major (Fortran-style) memory representation. Defaults to ‘C’.

out : ndarray

Array interpretation of a. No copy is performed if the input is already an ndarray. If a is a subclass of ndarray, a base class ndarray is returned.

asanyarray : Similar function which passes through subclasses. ascontiguousarray : Convert input to a contiguous array. asfarray : Convert input to a floating point ndarray. asfortranarray : Convert input to an ndarray with column-major

memory order.

asarray_chkfinite : Similar function which checks input for NaNs and Infs. fromiter : Create an array from an iterator. fromfunction : Construct an array by executing a function on grid

positions.

Convert a list into an array:

>>> a = [1, 2]
>>> np.asarray(a)
array([1, 2])

Existing arrays are not copied:

>>> a = np.array([1, 2])
>>> np.asarray(a) is a
True

If dtype is set, array is copied only if dtype does not match:

>>> a = np.array([1, 2], dtype=np.float32)
>>> np.asarray(a, dtype=np.float32) is a
True
>>> np.asarray(a, dtype=np.float64) is a
False

Contrary to asanyarray, ndarray subclasses are not passed through:

>>> issubclass(np.matrix, np.ndarray)
True
>>> a = np.matrix([[1, 2]])
>>> np.asarray(a) is a
False
>>> np.asanyarray(a) is a
True

Minimize a function over a given range by brute force.

func : callable f(x,*args)

Objective function to be minimized.

ranges : tuple

Each element is a tuple of parameters or a slice object to be handed to numpy.mgrid.

args : tuple

Extra arguments passed to function.

Ns : int

Default number of samples, if those are not provided.

full_output : bool

If True, return the evaluation grid.

finish : callable, optional

An optimization function that is called with the result of brute force minimization as initial guess. finish should take the initial guess as positional argument, and take take args, full_output and disp as keyword arguments. See Notes for more details.

disp : bool, optional

Set to True to print convergence messages.

x0 : ndarray

Value of arguments to func, giving minimum over the grid.

fval : int

Function value at minimum.

grid : tuple

Representation of the evaluation grid. It has the same length as x0.

Jout : ndarray

Function values over grid: Jout = func(*grid).

The range is respected by the brute force minimization, but if the finish keyword specifies another optimization function (including the default fmin), the returned value may still be (just) outside the range. In order to ensure the range is specified, use finish=None.

A generic brute-force grid-search error minimization function.

The user specifies an objective_function and the corresponding args for generating a model prediction. The brute_force_search uses search_bounds to dictate the bounds for evenly sample the parameter space.

In addition, the user must also supply fit_bounds, containing pairs of upper and lower bounds for each of the values in parameters. If fit_bounds is specified, the error minimization procedure in error_function will return an Inf whether the parameters exceed the minimum or maxmimum values specified in fit_bounds.

The output of brute_force_search can be used as a seed-point for the fine-tuned solutions from gradient_descent_search.

args : tuple

Arguments to objective_function that yield a model prediction.

grids : tuple

A tuple indicating the search space for the brute-force grid-search. The tuple contains pairs of upper and lower bounds for exploring a given dimension. For example grids=((-10,10),(0,5),) will search the first dimension from -10 to 10 and the second from 0 to 5. These values cannot be None.

For more information, see scipy.optimize.brute.

bounds : tuple

A tuple containing the upper and lower bounds for each parameter in parameters. If a parameter is not bounded, simply use None. For example, fit_bounds=((0,None),(-10,10),) would bound the first parameter to be any positive number while the second parameter would be bounded between -10 and 10.

Ns : int

Number of samples per stimulus dimension to sample during the ballpark search.

For more information, see scipy.optimize.brute.

data : ndarray

The actual, measured time-series against which the model is fit.

error_function : callable

The error function that relates the model prediction to the measure data. The error function returns a float that represents the residual sum of squared errors between the prediction and the data.

objective_function : callable

The objective function that takes parameters and args and proceduces a model time-series.

estimate : tuple

The model solution given parameters and objective_function.

Assumes that the 0th and 1st parameters are cartesian x and y

Compute the determinant of a matrix

The determinant of a square matrix is a value derived arithmetically from the coefficients of the matrix.

The determinant for a 3x3 matrix, for example, is computed as follows:

a    b    c
d    e    f = A
g    h    i

det(A) = a*e*i + b*f*g + c*d*h - c*e*g - b*d*i - a*f*h

a : (M, M) array_like

A square matrix.

overwrite_a : bool

Allow overwriting data in a (may enhance performance).

check_finite : boolean, optional

Whether to check the input matrixes contain only finite numbers. Disabling may give a performance gain, but may result to problems (crashes, non-termination) if the inputs do contain infinities or NaNs.

det : float or complex

Determinant of a.

The determinant is computed via LU factorization, LAPACK routine z/dgetrf.

>>> a = np.array([[1,2,3],[4,5,6],[7,8,9]])
>>> linalg.det(a)
0.0
>>> a = np.array([[0,2,3],[4,5,6],[7,8,9]])
>>> linalg.det(a)
3.0

Return specified diagonals.

If a is 2-D, returns the diagonal of a with the given offset, i.e., the collection of elements of the form a[i, i+offset]. If a has more than two dimensions, then the axes specified by axis1 and axis2 are used to determine the 2-D sub-array whose diagonal is returned. The shape of the resulting array can be determined by removing axis1 and axis2 and appending an index to the right equal to the size of the resulting diagonals.

In versions of NumPy prior to 1.7, this function always returned a new, independent array containing a copy of the values in the diagonal.

In NumPy 1.7 and 1.8, it continues to return a copy of the diagonal, but depending on this fact is deprecated. Writing to the resulting array continues to work as it used to, but a FutureWarning is issued.

Starting in NumPy 1.9 it returns a read-only view on the original array. Attempting to write to the resulting array will produce an error.

In some future release, it will return a read/write view and writing to the returned array will alter your original array. The returned array will have the same type as the input array.

If you don’t write to the array returned by this function, then you can just ignore all of the above.

If you depend on the current behavior, then we suggest copying the returned array explicitly, i.e., use np.diagonal(a).copy() instead of just np.diagonal(a). This will work with both past and future versions of NumPy.

a : array_like

Array from which the diagonals are taken.

offset : int, optional

Offset of the diagonal from the main diagonal. Can be positive or negative. Defaults to main diagonal (0).

axis1 : int, optional

Axis to be used as the first axis of the 2-D sub-arrays from which the diagonals should be taken. Defaults to first axis (0).

axis2 : int, optional

Axis to be used as the second axis of the 2-D sub-arrays from which the diagonals should be taken. Defaults to second axis (1).

array_of_diagonals : ndarray

If a is 2-D and not a matrix, a 1-D array of the same type as a containing the diagonal is returned. If a is a matrix, a 1-D array containing the diagonal is returned in order to maintain backward compatibility. If the dimension of a is greater than two, then an array of diagonals is returned, “packed” from left-most dimension to right-most (e.g., if a is 3-D, then the diagonals are “packed” along rows).

ValueError

If the dimension of a is less than 2.

diag : MATLAB work-a-like for 1-D and 2-D arrays. diagflat : Create diagonal arrays. trace : Sum along diagonals.

>>> a = np.arange(4).reshape(2,2)
>>> a
array([[0, 1],
       [2, 3]])
>>> a.diagonal()
array([0, 3])
>>> a.diagonal(1)
array([1])

A 3-D example:

>>> a = np.arange(8).reshape(2,2,2); a
array([[[0, 1],
        [2, 3]],
       [[4, 5],
        [6, 7]]])
>>> a.diagonal(0, # Main diagonals of two arrays created by skipping
...            0, # across the outer(left)-most axis last and
...            1) # the "middle" (row) axis first.
array([[0, 6],
       [1, 7]])

The sub-arrays whose main diagonals we just obtained; note that each corresponds to fixing the right-most (column) axis, and that the diagonals are “packed” in rows.

>>> a[:,:,0] # main diagonal is [0 6]
array([[0, 2],
       [4, 6]])
>>> a[:,:,1] # main diagonal is [1 7]
array([[1, 3],
       [5, 7]])

Calculate the n-th discrete difference along given axis.

The first difference is given by out[n] = a[n+1] - a[n] along the given axis, higher differences are calculated by using diff recursively.

a : array_like

Input array

n : int, optional

The number of times values are differenced.

axis : int, optional

The axis along which the difference is taken, default is the last axis.

diff : ndarray

The n-th differences. The shape of the output is the same as a except along axis where the dimension is smaller by n.

.

gradient, ediff1d, cumsum

>>> x = np.array([1, 2, 4, 7, 0])
>>> np.diff(x)
array([ 1,  2,  3, -7])
>>> np.diff(x, n=2)
array([  1,   1, -10])

>>> x = np.array([[1, 3, 6, 10], [0, 5, 6, 8]])
>>> np.diff(x)
array([[2, 3, 4],
       [5, 1, 2]])
>>> np.diff(x, axis=0)
array([[-1,  2,  0, -2]])

Dot product of two arrays.

For 2-D arrays it is equivalent to matrix multiplication, and for 1-D arrays to inner product of vectors (without complex conjugation). For N dimensions it is a sum product over the last axis of a and the second-to-last of b:

dot(a, b)[i,j,k,m] = sum(a[i,j,:] * b[k,:,m])

a : array_like

First argument.

b : array_like

Second argument.

out : ndarray, optional

Output argument. This must have the exact kind that would be returned if it was not used. In particular, it must have the right type, must be C-contiguous, and its dtype must be the dtype that would be returned for dot(a,b). This is a performance feature. Therefore, if these conditions are not met, an exception is raised, instead of attempting to be flexible.

output : ndarray

Returns the dot product of a and b. If a and b are both scalars or both 1-D arrays then a scalar is returned; otherwise an array is returned. If out is given, then it is returned.

ValueError

If the last dimension of a is not the same size as the second-to-last dimension of b.

vdot : Complex-conjugating dot product. tensordot : Sum products over arbitrary axes. einsum : Einstein summation convention. matmul : ‘@’ operator as method with out parameter.

>>> np.dot(3, 4)
12

Neither argument is complex-conjugated:

>>> np.dot([2j, 3j], [2j, 3j])
(-13+0j)

For 2-D arrays it is the matrix product:

>>> a = [[1, 0], [0, 1]]
>>> b = [[4, 1], [2, 2]]
>>> np.dot(a, b)
array([[4, 1],
       [2, 2]])

>>> a = np.arange(3*4*5*6).reshape((3,4,5,6))
>>> b = np.arange(3*4*5*6)[::-1].reshape((5,4,6,3))
>>> np.dot(a, b)[2,3,2,1,2,2]
499128
>>> sum(a[2,3,2,:] * b[1,2,:,2])
499128

The double gamma hemodynamic reponse function (HRF). The user specifies only the delay of the peak and undershoot. The delay shifts the peak and undershoot by a variable number of seconds. The other parameters are hardcoded. The HRF delay is modeled for each voxel independently. The form of the HRF and the hardcoded values are based on previous work [1]_.

delay : float

The delay of the HRF peak and undershoot.

tr : float

The length of the repetition time in seconds.

fptr : float

The number of stimulus frames per reptition time. For a 60 Hz projector and with a 1 s repetition time, the fptr would be equal to 60. It is possible that you will bin all the frames in a single TR, in which case fptr equals 1.

integrator : callable

The integration function for normalizing the units of the HRF so that the area under the curve is the same for differently delayed HRFs. Set integrator to None to turn off normalization.

hrf : ndarray

The hemodynamic response function to convolve with the stimulus timeseries.

BOLD fMRI. NeuroImage 9, 416-429.

A generic error function with bounding.

parameters : tuple

A tuple of values representing a model setting.

args : tuple

Extra arguments to objective_function beyond those in parameters.

data : ndarray

The actual, measured time-series against which the model is fit.

objective_function : callable

The objective function that takes parameters and args and proceduces a model time-series.

debug : bool

Useful for debugging a model, will print the parameters and error.

error : float

The residual sum of squared errors between the prediction and data.

Minimize a function using the downhill simplex algorithm.

This algorithm only uses function values, not derivatives or second derivatives.

func : callable func(x,*args)

The objective function to be minimized.

x0 : ndarray

Initial guess.

args : tuple, optional

Extra arguments passed to func, i.e. f(x,*args).

callback : callable, optional

Called after each iteration, as callback(xk), where xk is the current parameter vector.

xtol : float, optional

Relative error in xopt acceptable for convergence.

ftol : number, optional

Relative error in func(xopt) acceptable for convergence.

maxiter : int, optional

Maximum number of iterations to perform.

maxfun : number, optional

Maximum number of function evaluations to make.

full_output : bool, optional

Set to True if fopt and warnflag outputs are desired.

disp : bool, optional

Set to True to print convergence messages.

retall : bool, optional

Set to True to return list of solutions at each iteration.

xopt : ndarray

Parameter that minimizes function.

fopt : float

Value of function at minimum: fopt = func(xopt).

iter : int

Number of iterations performed.

funcalls : int

Number of function calls made.

warnflag : int

1 : Maximum number of function evaluations made. 2 : Maximum number of iterations reached.

allvecs : list

Solution at each iteration.

minimize: Interface to minimization algorithms for multivariate

functions. See the ‘Nelder-Mead’ method in particular.

Uses a Nelder-Mead simplex algorithm to find the minimum of function of one or more variables.

This algorithm has a long history of successful use in applications. But it will usually be slower than an algorithm that uses first or second derivative information. In practice it can have poor performance in high-dimensional problems and is not robust to minimizing complicated functions. Additionally, there currently is no complete theory describing when the algorithm will successfully converge to the minimum, or how fast it will if it does.

Minimize a function using modified Powell’s method. This method only uses function values, not derivatives.

func : callable f(x,*args)

Objective function to be minimized.

x0 : ndarray

Initial guess.

args : tuple, optional

Extra arguments passed to func.

callback : callable, optional

An optional user-supplied function, called after each iteration. Called as callback(xk), where xk is the current parameter vector.

direc : ndarray, optional

Initial direction set.

xtol : float, optional

Line-search error tolerance.

ftol : float, optional

Relative error in func(xopt) acceptable for convergence.

maxiter : int, optional

Maximum number of iterations to perform.

maxfun : int, optional

Maximum number of function evaluations to make.

full_output : bool, optional

If True, fopt, xi, direc, iter, funcalls, and warnflag are returned.

disp : bool, optional

If True, print convergence messages.

retall : bool, optional

If True, return a list of the solution at each iteration.

xopt : ndarray

Parameter which minimizes func.

fopt : number

Value of function at minimum: fopt = func(xopt).

direc : ndarray

Current direction set.

iter : int

Number of iterations.

funcalls : int

Number of function calls made.

warnflag : int

Integer warning flag:

1 : Maximum number of function evaluations. 2 : Maximum number of iterations.

allvecs : list

List of solutions at each iteration.

minimize: Interface to unconstrained minimization algorithms for

multivariate functions. See the ‘Powell’ method in particular.

Uses a modification of Powell’s method to find the minimum of a function of N variables. Powell’s method is a conjugate direction method.

The algorithm has two loops. The outer loop merely iterates over the inner loop. The inner loop minimizes over each current direction in the direction set. At the end of the inner loop, if certain conditions are met, the direction that gave the largest decrease is dropped and replaced with the difference between the current estiamted x and the estimated x from the beginning of the inner-loop.

The technical conditions for replacing the direction of greatest increase amount to checking that

1. No further gain can be made along the direction of greatest increase from that iteration.
2. The direction of greatest increase accounted for a large sufficient fraction of the decrease in the function value from that iteration of the inner loop.

Powell M.J.D. (1964) An efficient method for finding the minimum of a function of several variables without calculating derivatives, Computer Journal, 7 (2):155-162.

Press W., Teukolsky S.A., Vetterling W.T., and Flannery B.P.: Numerical Recipes (any edition), Cambridge University Press

Creates synchronized shared arrays from numpy arrays.

The function takes a numpy array unshared_arr and returns a shared memory object, shared_arr. The user also specifies the data-type of the values in the array with the dataType argument. See multiprocessing.Array and ctypes for details on shared memory arrays and the data-types.

unshared_arr : ndarray

Array_like means all those objects – lists, nested lists, etc. – that can be converted to an array. We can also refer to variables like var1.

dtype : ctypes instance

The data-type specificed has to be an instance of the ctypes library. See ctypes for details.

shared_arr : synchronized shared array

An array that is read accessible from multiple processes/threads.

A generic gradient-descent error minimization function.

The values inside parameters are used as a seed-point for a gradient-descent error minimization procedure [1]_. The user must also supply an objective_function for producing a model prediction and an error_function for relating that prediction to the actual, measured data.

In addition, the user may also supply fit_bounds, containing pairs of upper and lower bounds for each of the values in parameters. If fit_bounds is specified, the error minimization procedure in error_function will return an Inf whether the parameters exceed the minimum or maxmimum values specified in fit_bounds.

parameters : tuple

A tuple of values representing a model setting.

args : tuple

Extra arguments to objective_function beyond those in parameters.

fit_bounds : tuple

A tuple containing the upper and lower bounds for each parameter in parameters. If a parameter is not bounded, simply use None. For example, fit_bounds=((0,None),(-10,10),) would bound the first parameter to be any positive number while the second parameter would be bounded between -10 and 10.

data : ndarray

The actual, measured time-series against which the model is fit.

error_function : callable

The error function that relates the model prediction to the measure data. The error function returns a float that represents the residual sum of squared errors between the prediction and the data.

objective_function : callable

The objective function that takes parameters and args and proceduces a model time-series.

estimate : tuple

The model solution given parameters and objective_function.

method for minimization, Compututation Journal 6, 163-168.

Compute the inverse of a matrix.

a : array_like

Square matrix to be inverted.

overwrite_a : bool, optional

Discard data in a (may improve performance). Default is False.

check_finite : boolean, optional

Whether to check the input matrixes contain only finite numbers. Disabling may give a performance gain, but may result to problems (crashes, non-termination) if the inputs do contain infinities or NaNs.

ainv : ndarray

Inverse of the matrix a.

LinAlgError :

If a is singular.

ValueError :

If a is not square, or not 2-dimensional.

>>> a = np.array([[1., 2.], [3., 4.]])
>>> sp.linalg.inv(a)
array([[-2. ,  1. ],
       [ 1.5, -0.5]])
>>> np.dot(a, sp.linalg.inv(a))
array([[ 1.,  0.],
       [ 0.,  1.]])

Returns True if the type of num is a scalar type.

num : any

Input argument, can be of any type and shape.

val : bool

True if num is a scalar type, False if it is not.

>>> np.isscalar(3.1)
True
>>> np.isscalar([3.1])
False
>>> np.isscalar(False)
True

A short-hand function for normalizing an array to a desired range.

array : ndarray

An array to be normalized.

imin : float

The desired minimum value in the output array. Default: -1

imax : float

The desired maximum value in the output array. Default: 1

array : ndarray

The normalized array with imin and imax as the minimum and maximum values.

Return a new array of given shape and type, filled with ones.

shape : int or sequence of ints

Shape of the new array, e.g., (2, 3) or 2.

dtype : data-type, optional

The desired data-type for the array, e.g., numpy.int8. Default is numpy.float64.

order : {‘C’, ‘F’}, optional

Whether to store multidimensional data in C- or Fortran-contiguous (row- or column-wise) order in memory.

out : ndarray

Array of ones with the given shape, dtype, and order.

zeros, ones_like

>>> np.ones(5)
array([ 1.,  1.,  1.,  1.,  1.])

>>> np.ones((5,), dtype=np.int)
array([1, 1, 1, 1, 1])

>>> np.ones((2, 1))
array([[ 1.],
       [ 1.]])

>>> s = (2,2)
>>> np.ones(s)
array([[ 1.,  1.],
       [ 1.,  1.]])

This is a convenience function for parallelizing the fitting procedure. Each call is handed a tuple or list containing all the necessary inputs for instantiaing a GaussianFit class object and estimating the model parameters.

args : list/tuple

A list or tuple containing all the necessary inputs for fitting the Gaussian pRF model.

fit : Fit class object

A fit object that contains all the inputs and outputs of the pRF model estimation for a single voxel.

Converted from MATLAB script at http://billauer.co.il/peakdet.html

Returns two arrays

function [maxtab, mintab]=peakdet(v, delta, x) #PEAKDET Detect peaks in a vector # [MAXTAB, MINTAB] = PEAKDET(V, DELTA) finds the local # maxima and minima (“peaks”) in the vector V. # MAXTAB and MINTAB consists of two columns. Column 1 # contains indices in V, and column 2 the found values. # # With [MAXTAB, MINTAB] = PEAKDET(V, DELTA, X) the indices # in MAXTAB and MINTAB are replaced with the corresponding # X-values. # # A point is considered a maximum peak if it has the maximal # value, and was preceded (to the left) by a value lower by # DELTA. # # Eli Billauer, 3.4.05 (Explicitly not copyrighted). # This function is released to the public domain; Any use is allowed.

Returns the % signal change of each point of the times series along a given axis of the array timeseries

ts : ndarray

an array of time series

ax : int, optional (default to -1)

the axis of time_series along which to compute means and stdevs

ndarray

the renormalized time series array (in units of %)

>>> np.set_printoptions(precision=4)  # for doctesting
>>> ts = np.arange(4*5).reshape(4,5)
>>> ax = 0
>>> percent_change(ts,ax)
array([[-100.    ,  -88.2353,  -78.9474,  -71.4286,  -65.2174],
       [ -33.3333,  -29.4118,  -26.3158,  -23.8095,  -21.7391],
       [  33.3333,   29.4118,   26.3158,   23.8095,   21.7391],
       [ 100.    ,   88.2353,   78.9474,   71.4286,   65.2174]])
>>> ax = 1
>>> percent_change(ts,ax)
array([[-100.    ,  -50.    ,    0.    ,   50.    ,  100.    ],
       [ -28.5714,  -14.2857,    0.    ,   14.2857,   28.5714],
       [ -16.6667,   -8.3333,    0.    ,    8.3333,   16.6667],
       [ -11.7647,   -5.8824,    0.    ,    5.8824,   11.7647]])

Return a sample (or samples) from the “standard normal” distribution.

If positive, int_like or int-convertible arguments are provided, randn generates an array of shape (d0, d1, ..., dn), filled with random floats sampled from a univariate “normal” (Gaussian) distribution of mean 0 and variance 1 (if any of the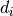 are floats, they are first converted to integers by truncation). A single float randomly sampled from the distribution is returned if no argument is provided.

This is a convenience function. If you want an interface that takes a tuple as the first argument, use numpy.random.standard_normal instead.

d0, d1, ..., dn : int, optional

The dimensions of the returned array, should be all positive. If no argument is given a single Python float is returned.

Z : ndarray or float

A (d0, d1, ..., dn)-shaped array of floating-point samples from the standard normal distribution, or a single such float if no parameters were supplied.

random.standard_normal : Similar, but takes a tuple as its argument.

For random samples from 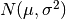, use:

sigma * np.random.randn(...) + mu

>>> np.random.randn()
2.1923875335537315 #random

Two-by-four array of samples from N(3, 6.25):

>>> 2.5 * np.random.randn(2, 4) + 3
array([[-4.49401501,  4.00950034, -1.81814867,  7.29718677],  #random
       [ 0.39924804,  4.68456316,  4.99394529,  4.84057254]]) #random

Romberg integration using samples of a function.

y : array_like

A vector of 2**k + 1 equally-spaced samples of a function.

dx : array_like, optional

The sample spacing. Default is 1.

axis : array_like?, optional

The axis along which to integrate. Default is -1 (last axis).

show : bool, optional

When y is a single 1-D array, then if this argument is True print the table showing Richardson extrapolation from the samples. Default is False.

ret : array_like?

The integrated result for each axis.

quad - adaptive quadrature using QUADPACK romberg - adaptive Romberg quadrature quadrature - adaptive Gaussian quadrature fixed_quad - fixed-order Gaussian quadrature dblquad, tplquad - double and triple integrals simps, trapz - integrators for sampled data cumtrapz - cumulative integration for sampled data ode, odeint - ODE integrators

Seed the generator.

This method is called when RandomState is initialized. It can be called again to re-seed the generator. For details, see RandomState.

seed : int or array_like, optional

Seed for RandomState. Must be convertible to 32 bit unsigned integers.

RandomState

x, random=random.random -> shuffle list x in place; return None.

Optional arg random is a 0-argument function returning a random float in [0.0, 1.0); by default, the standard random.random.

Solve the equation a x = b for x.

a : (M, M) array_like

A square matrix.

b : (M,) or (M, N) array_like

Right-hand side matrix in a x = b.

sym_pos : bool

Assume a is symmetric and positive definite.

lower : boolean

Use only data contained in the lower triangle of a, if sym_pos is true. Default is to use upper triangle.

overwrite_a : bool

Allow overwriting data in a (may enhance performance). Default is False.

overwrite_b : bool

Allow overwriting data in b (may enhance performance). Default is False.

check_finite : boolean, optional

Whether to check the input matrixes contain only finite numbers. Disabling may give a performance gain, but may result to problems (crashes, non-termination) if the inputs do contain infinities or NaNs.

x : (M,) or (M, N) ndarray

Solution to the system a x = b. Shape of the return matches the shape of b.

LinAlgError

If a is singular.

Given a and b, solve for x:

>>> a = np.array([[3,2,0],[1,-1,0],[0,5,1]])
>>> b = np.array([2,4,-1])
>>> x = linalg.solve(a,b)
>>> x
array([ 2., -2.,  9.])
>>> np.dot(a, x) == b
array([ True,  True,  True], dtype=bool)

An implementation of spm_hrf.m from the SPM distribution

Arguments:

Required: TR: repetition time at which to generate the HRF (in seconds)

Optional: p: list with parameters of the two gamma functions:

defaults

(seconds)

p[0] - delay of response (relative to onset) 6 p[1] - delay of undershoot (relative to onset) 16 p[2] - dispersion of response 1 p[3] - dispersion of undershoot 1 p[4] - ratio of response to undershoot 6 p[5] - onset (seconds) 0 p[6] - length of kernel (seconds) 32

Integrate along the given axis using the composite trapezoidal rule.

Integrate y (x) along given axis.

y : array_like

Input array to integrate.

x : array_like, optional

The sample points corresponding to the y values. If x is None, the sample points are assumed to be evenly spaced dx apart. The default is None.

dx : scalar, optional

The spacing between sample points when x is None. The default is 1.

axis : int, optional

The axis along which to integrate.

trapz : float

Definite integral as approximated by trapezoidal rule.

sum, cumsum

Image [2]_ illustrates trapezoidal rule – y-axis locations of points will be taken from y array, by default x-axis distances between points will be 1.0, alternatively they can be provided with x array or with dx scalar. Return value will be equal to combined area under the red lines.

>>> np.trapz([1,2,3])
4.0
>>> np.trapz([1,2,3], x=[4,6,8])
8.0
>>> np.trapz([1,2,3], dx=2)
8.0
>>> a = np.arange(6).reshape(2, 3)
>>> a
array([[0, 1, 2],
       [3, 4, 5]])
>>> np.trapz(a, axis=0)
array([ 1.5,  2.5,  3.5])
>>> np.trapz(a, axis=1)
array([ 2.,  8.])

Returns the z-score of each point of the time series along a given axis of the array time_series.

time_series : ndarray

an array of time series

axis : int, optional

the axis of time_series along which to compute means and stdevs

zt : ndarray

the renormalized time series array